Answer:
Probability of getting a sample with 14% rebellious humans or more is 0.0104.
Explanation:
We are given that an alien empire is considering taking over planet Earth, but they will only do so if the portion of rebellious humans is less than 10%.
They abducted a random sample of 400 humans, performed special psychological tests, and found that 14% of the sample are rebellious.
Let p = population proportion rebellious humans
The z score probability distribution for sample proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,

 = sample proportion rebellious humans = 14%
= sample proportion rebellious humans = 14%
n = sample of humans = 400
p = population proportion rebellious humans = 10%
Now, probability of getting a sample with 14% rebellious humans or more is given by = P(

 14%)
14%)
P(

 0.14) = P(
0.14) = P(


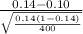 ) = P(Z
) = P(Z
 2.31)
2.31)
= 1 - P(Z < 2.31) = 1 - 0.9896 = 0.0104
The above probability is calculated by looking at the value of x = 2.31 in the z table which has an area of 0.9896.
Hence, the required probability is 0.0104.