Answer:
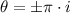 ,
,

Explanation:
The determination of the maximum can be done with the help of the First and Second Derivative Tests. The first and second derivatives of the function are, respectively:
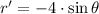
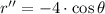
First Derivative Test
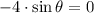
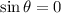
Given the periodicity of the function, there are multiple solutions. The set of solutions is represented by:
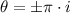 ,
,
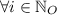
Second Derivative Test
There are multiple solutions. If
 is an odd number, then cosine is negative and output is positive, which means that associated value is an absolute minimum. Otherwise, if
is an odd number, then cosine is negative and output is positive, which means that associated value is an absolute minimum. Otherwise, if
 is zero or an even number, the cosine is positive and output is negative, which means that associated value is an absolute minimum. Consequently, the values of
is zero or an even number, the cosine is positive and output is negative, which means that associated value is an absolute minimum. Consequently, the values of
 so that
so that
 is a maximum are:
is a maximum are:
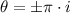 ,
,
