Question

The product of (x+p)(x+q) can be written as x^2+(p+q)x+pq.

An intermediate step in this multiplication is
x^2+px+qx+pq=x^2+(p+q)x+pq.
Explain why px+qx=(p+q)x.
I'm Really confused please help!

Answer 1

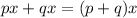`px+qx=(p+q)x` by taking out the common factors.

Explanation:

It is given that the product of
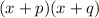`(x+p)(x+q)` is
`x^2+(p+q)x+pq`.

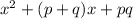Given expression is

`(x+p)(x+q)`

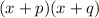
Using distributive property, we get

`x(x+q)+p(x+q)`

`x(x)+q(x)+p(x)+p(q)`

`x^2+qx+px+pq`

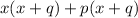
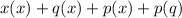
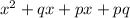
In middle terms px and qx the highest common factor is x. So taking out common factor from middle terms we get

`x^2+x(q+p)+pq`

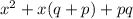
It can be written as

`x^2+x(p+q)+pq`

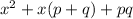
Therefore,
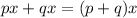`px+qx=(p+q)x` by taking out the common factors.