Question

Given the information below, write the conclusion in context. 1. H0 : The proportion of defective batteries = 0.02 2. HA : The proportion of defective batteries < 0.02 3. Z-score of observed sample = −1.23

Answer 1

`z = -1.23`

And we can calculate the p value with the following probability taking in count the alternative hypothesis:

`p_v = P(z<-1.23) = 0.1093`

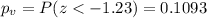
And for this case using a significance level of
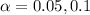`\alpha=0.05 ,0.1` we see that the p value is larger than the significance level so then we can conclude that we FAIL to reject the null hypothesis and we don't have enough evidence to conclude that the true proportion is less than 0.02

Explanation:

For this case we want to test the following system of hypothesis:

Null hypothesis:
`p =0.02`

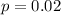
Alternative hypothesis:
`p < 0.02`

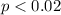
The statistic for this case is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

And for this case we know that the statistic is given by:

`z = -1.23`

And we can calculate the p value with the following probability taking in count the alternative hypothesis:

`p_v = P(z<-1.23) = 0.1093`

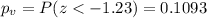
And for this case using a significance level of
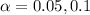`\alpha=0.05 ,0.1` we see that the p value is larger than the significance level so then we can conclude that we FAIL to reject the null hypothesis and we don't have enough evidence to conclude that the true proportion is less than 0.02