Question

A cosine function is a reflection of its parent function over the x-axis. The amplitude of the function is 11, the vertical shift is 9 units down, and the period of the function is 7pi/12. The graph of the function does not show a phase shift. What is the equation of the cosine function described?

Fill in the blanks using values from this list: -20, -11, -9, -2, 2, 9, 11, 20, 7pi/12,12pi/7,7/24,24/7

f(x)=___cos(_____x)______

Answer 1

We have been given that a cosine function is a reflection of its parent function over the x-axis. The amplitude of the function is 11, the vertical shift is 9 units down, and the period of the function is
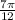`(7\pi)/(12)`. The graph of the function does not show a phase shift. We are asked to write the equation of our function.

We know that general form a cosine function is
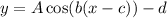`y=A\cos(b(x-c))-d`, where,

A = Amplitude,

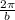`(2\pi)/(b)` = Period,

c = Horizontal shift,

d = Vertical shift.

The equation of parent cosine function is
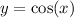`y=\cos(x)`. Since function is reflected about x-axis, so our function will be
`y=-\cos(x)`.

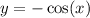Let us find the value of b.

`(2\pi)/(b)=(7\pi)/(12)`

`7\pi\cdot b=24\pi`

`(7\pi\cdot b)/(7\pi)=(24\pi)/(7\pi)`

`b=(24)/(7)`

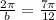
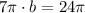
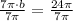
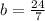
Upon substituting our given values in general cosine function, we will get:

`f(x)=-11\cos((24)/(7)x)-9`

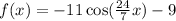
Therefore, our required function would be
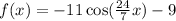`f(x)=-11\cos((24)/(7)x)-9`.