Answer:
Since
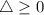 , the superhero makes it over the building.
, the superhero makes it over the building.
Explanation:
The height is given by the following function:
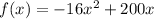
Will the superhero make it over the building?
We have to find if there is values of x for which f(x) = 612.
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
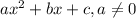 .
.
This polynomial has roots
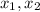 such that
such that
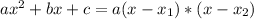 , given by the following formulas:
, given by the following formulas:
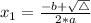
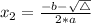

If
 , the polynomial has no solutions.
, the polynomial has no solutions.
In this question:
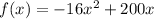

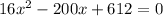
We have to find

We have that
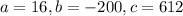 . So
. So
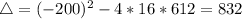
Since
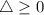 , the superhero makes it over the building.
, the superhero makes it over the building.