Question

If a cylinder has a volume of 1884 cubic centimeters and a height of six cm, explain how to find the radius of the

base circle.

Answer 1

10 cm

Explanation:

The volume of the cylinder is 1884 cubic centimetres and its height is 6 cm.

The volume of a cylinder is given as:

`V = \pi r^2 h`

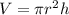
where r = radius

h = height

To find the radius of the base of the cylinder, we make r the subject of the formula and solve it:

`V = \pi r^2 h`

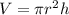
Divide both sides by πh:

`(V)/(\pi h) = (\pi r^2h)/(\pi h) \\\\=> (V)/(\pi h) = r^2`

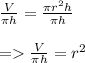
Find the square root of both sides:

`\sqrt{(V)/(\pi h)} = √(r^2) \\\\=> r = \sqrt{(V)/(\pi h)}`

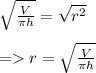
Let us find the value of r:

`r = \sqrt{(1884)/(\pi * 6)}\\\\r = √(99.9493) \\`

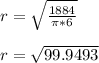
=> r = 9.9975 cm ≅ 10 cm