Question

If n = 580 and X = 464, construct a 90% confidence interval for the population proportion, p.

Give your answers to three decimals



< p <

Answer 1

`0.80 - 1.64 \sqrt{(0.8(1-0.8))/(580)}=0.773`

`0.80 + 1.64 \sqrt{(0.8(1-0.8))/(580)}=0.827`

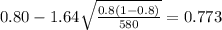
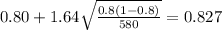
And the 90% confidence interval would be given (0.773;0.827).

Explanation:

The information given is:

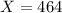`X = 464` represent the number of individuals with the characteristic

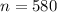`n = 580` the sample size

`\hat p =(X)/(n)= (464)/(580)= 0.8`

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

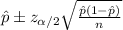
For the 90% confidence interval the value of
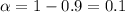`\alpha=1-0.9=0.1` and
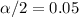`\alpha/2=0.05`, the critical value for this case is:

`z_(\alpha/2)=1.64`

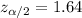
And replacing into the confidence interval formula we got:

`0.80 - 1.64 \sqrt{(0.8(1-0.8))/(580)}=0.773`

`0.80 + 1.64 \sqrt{(0.8(1-0.8))/(580)}=0.827`

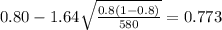
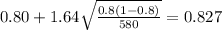
And the 90% confidence interval would be given (0.773;0.827).