Question

In 2002, the mean age of an inmate on death row was 40.7 years with a standard deviation of 9.6 years according to the U.S. Department of Justice. A sociologist wondered whether the mean age of a death-row inmate has changed since then. She randomly selects 32 death-row inmates and finds that their mean age is 38.9 years. Construct the 95% confidence interval for the current mean age of death-row inmates.

Answer 1

The 95% confidence interval for the current mean age of death-row inmates is between 42.23 years and 35.57 years.

Explanation:

The confidence interval of the mean is given by the next formula:

`\\ \overline{x} \pm z_{1-(\alpha)/(2)}(\sigma)/(√(n))` [1]

We already know (according to the U.S. Department of Justice):

• The (population) standard deviation for this case (mean age of an inmate on death row) has a standard deviation of 9.6 years (
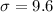  `\\ \sigma = 9.6`years).
• The number of observations for the sample taken is
  `\\ n = 32`.
• The sample mean,
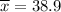  `\\ \overline{x} = 38.9` years.

For
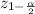`\\ z_{1-(\alpha)/(2)}`, we have that
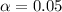`\\ \alpha = 0.05`. That is, the level of significance
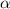`\\ \alpha` is 1 - 0.95 = 0.05. In this case, then, we have that the z-score corresponding to this case is:

`\\ z_{1-(\alpha)/(2)} = z_{1-(0.05)/(2)} = z_(1-0.025) = z_(0.975)`

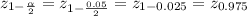
Consulting a cumulative standard normal table, available on the Internet or in Statistics books, to find the z-score associated to the probability of,
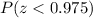`\\ P(z<0.975)`, we have that
`\\ z = 1.96`.

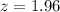Notice that we supposed that the sample is from a population that follows a normal distribution. However, we also have a value for n > 30, and we already know that for this result the sampling distribution for the sample means follows, approximately, a normal distribution with mean,
`\\ \mu`, and standard deviation,
`\\ \sigma_{\overline{x}} = (\sigma)/(√(n))`.

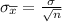Having all this information, we can proceed to answer the question.

Constructing the 95% confidence interval for the current mean age of death-row inmates

To construct the 95% confidence interval, we already know that this interval is given by [1]:

`\\ \overline{x} \pm z_{1-(\alpha)/(2)}(\sigma)/(√(n))`

That is, we have:

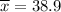`\\ \overline{x} = 38.9` years.

`\\ z_{1-(\alpha)/(2)} = 1.96`

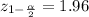
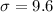`\\ \sigma = 9.6` years.

`\\ n = 32`

Then

`\\ 38.9 \pm 1.96*(9.6)/(√(32))`

`\\ 38.9 \pm 1.96*(9.6)/(5.656854)`

`\\ 38.9 \pm 1.96*1.697056`

`\\ 38.9 \pm 3.326229`

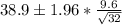
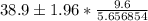
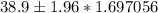
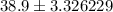
Therefore, the Upper and Lower limits of the interval are:

Upper limit:

`\\ 38.9 + 3.326229`

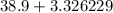
`\\ 42.226229 \approx 42.23` years.

Lower limit:

`\\ 38.9 - 3.326229`

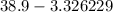
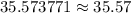`\\ 35.573771 \approx 35.57` years.

In sum, the 95% confidence interval for the current mean age of death-row inmates is between 42.23 years and 35.57 years.

Notice that the "mean age of an inmate on death row was 40.7 years in 2002", and this value is between the limits of the 95% confidence interval obtained. So, according to the random sample under study, it seems that this mean age has not changed.