Complete Question
In order to comply with the requirement that energy be conserved, Einstein showed in the photoelectric effect that the energy of a photon (h) absorbed by a metal is the sum of the work function (
 ), the minimum energy needed to dislodge an electron from the metal's surface, and the kinetic energy (Ek) of the electron:
), the minimum energy needed to dislodge an electron from the metal's surface, and the kinetic energy (Ek) of the electron:
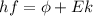 . When light of wavelength 357.4 nm falls on the surface of potassium metal, the speed (u) of the dislodged electron is 5.8×105 m/s. What is work function (in kJ/mol) of potassium?
. When light of wavelength 357.4 nm falls on the surface of potassium metal, the speed (u) of the dislodged electron is 5.8×105 m/s. What is work function (in kJ/mol) of potassium?
Answer:
The work function is

Step-by-step explanation:
From the question we are told that
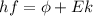
Where h is the Planck's constant which has a constant value of

Ek is the kinetic energy which is mathematically represented as

Where m is the mass of electron with a constant value

The wavelength is
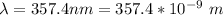
The speed of the electron is

This photoelectric effect can be mathematically defined as
f is the frequency of the incident light which is mathematically represented as
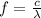
 is the work function
is the work function
So we have
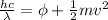
substituting value
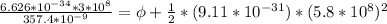

=>
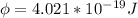
For one mole of one mole the work function is
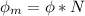
Where N is the avogadro's constant with a value

So
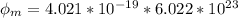

now in KJ
