Question

What is the arc length of a segment of a circle with a central angle of 165º and a radius of 3 inches?

Answer 1

D

Explanation:

Edge 2020

Answer 2

The exact value for the length of the arc is:
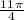`(11\,\pi)/(4)` inches, which is approximately 8.64 inches

Explanation:

We can solve this with proportions, knowing that the full circumference of the circle, which corresponds to an arc length of
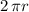`2\,\pi r`, is associated with
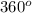`360^o`. Then we solve for the unknown arc length "x" for a subtended angle of
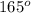`165^o` in the proportion:

`(2\,\pi r)/(360^o) = (x)/(165^o) \\(2\,\pi (3))/(360^o) = (x)/(165^o)\\x=(6\,\pi\,(165^o))/(360^o) \\x=(11\,\pi)/(4)`

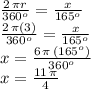
Which is approximately 8.64 inches