Question

In October 1947, the Gallup organization surveyed 1100 adult Americans and asked "Are you a total abstainer from, or do you on occasion consume alcoholic beverages?". Of the 1100 adults surveyed, 407 indicated that they were total abstainers. In a recent survey, the same question was asked of 1100 adult Americans and 333 indicated that they were total abstainers. Has the proportion of adult Americans who totally abstain from alcohol changed? Use the ???? = 0.05 level of significance. (use the traditional method of hypothesis testing)

Answer 1

`z=\frac{0.37-0.303}{\sqrt{0.336(1-0.336)((1)/(1100)+(1)/(1100))}}=3.327` .

`p_v =2*P(Z>3.327)= 0.000878`

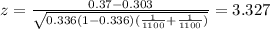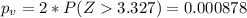
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true proportions for this case are different so then there is enough evidence to conlcude that the real proportion change.

Explanation:

Information provided

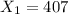`X_(1)=407` represent the number of people who answer abstainers in 1947

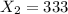`X_(2)=333` represent the number of people who answer abstainer recnetly

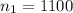`n_(1)=1100` sample 1 selected

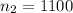`n_(2)=1100` sample 2 selected

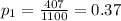`p_(1)=(407)/(1100)=0.37` represent the proportion estimated of people who answer abstainers in 1947

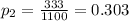`p_(2)=(333)/(1100)=0.303` represent the proportion estimated of people who answer abstainers recently

`\hat p` represent the pooled estimate of p

z would represent the statistic

`p_v` represent the p value

`\alpha=0.05` significance level given

Hypothesis to test

We want to verify if the proportion of adult Americans who totally abstain from alcohol changed , the system of hypothesis would be:

Null hypothesis:
`p_(1) = p_(2)`

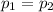
Alternative hypothesis:
`p_(1) \\eq p_(2)`

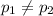
The statistic is given by:

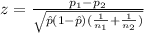`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(407+333)/(1100+1100)=0.336`

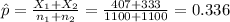
Replacing the info given we got:

`z=\frac{0.37-0.303}{\sqrt{0.336(1-0.336)((1)/(1100)+(1)/(1100))}}=3.327`

`p_v =2*P(Z>3.327)= 0.000878`

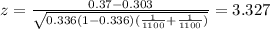
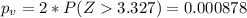
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis and we can conclude that the true proportions for this case are different so then there is enough evidence to conlcude that the real proportion change.