Question

In AWXY, the measure of ZY=90°, XW = 5, YX = 4, and WY = 3. What ratio

represents the cotangent of ZX?
X
5
4.
Y
W
3

Answer 1

Given:

In Δ
`WXY,m < Y=90^o,WY=3,XW=5` and
`YX=4`.

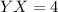To find:

The ratio represents the cosine of ∠
`W`.

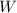Solution:

In Δ
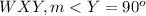`WXY,m < Y=90^o`. It means the opposite side of angle Y, i.e., XW is the hypotenuse of the triangle.

In a right angle triangle,

`cos0=(Base)/(Hypotenuse)`

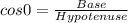
In the given triangle,

`cosW=(XY)/(YW)`

`cosW=(3)/(5)`

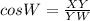
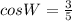
Therefore, the required cosine ratio is
`(3)/(5)`.