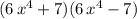Question

Use the formula a^2-b^2=(a+b)(a-b) to factor completely what are the factors of 36x^8-49

Answer 1

The factors are:
`(6\,x^4+7)(6\,x^4-7)`

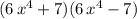
Explanation:

Start by trying to find how to write each term as a perfect square, that way you know what your "a" and "b" values should be.

Notice that:
`36\,x^8 = 6^2\,(x^4)^2 = (6\,x^4)^2`

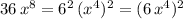
So, it is the perfect square of the quantity
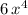`6\,x^4` (this is the "a" value that you need to use in your formula)

49 can also be written as a perfect square of 7:
`49=7^2`

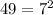
Therefore, 7 is the "b" value for the formula you are asked to use.

Now we can write:

`36\,x^8-49=(6\,x^4)^2-7^2`

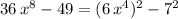
Then the formula goes as:

`a^2-b^2=(a+b)(a-b)\\(6\,x^4)^2-7^2=(6\,x^4+7)(6\,x^4-7)`

Then the factors we are looking for are:
`(6\,x^4+7)(6\,x^4-7)`