Question

The data below is a random sample of 3 observations drawn from the United States population. Use the data to answer the following questions:

i. Find 95% confidence intervals of the population mean of experience and wage.
ii. Estimate rhoe,w, the correlation between the variables experience and wage.
iii. Find βˆ 1 and βˆ 0, the estimates of the parameters in the following regression equation wage = β0 + β1education + ϵiv. Predict wages for a person with 15 years of education using your regression estimate.v. Find the R2wage education16.20 1212.36 1314.40 1212.00 12

Answer 1

Explanation:

Hello!

You have the data for 4 observations of randomly selected employees of the U.S.

Wage: 16.20; 12.36; 14.40; 12.00

Education: 12; 13; 12; 12

X₁: Wage of a U.S. employee.

X₂: Education of a U.S. employee.

i.

You have to estimate with a 95% confidence the population mean of each variable. Assuming all conditions are met, I'll use a students t to estimate both means.

* The general formula for the CI is: [X[bar]±
`t_(n-1;1-\alpha /2)`*
`(S)/(√(n) )`]

`t_(n-1;1-\alpha /2)= t_(3;0.975)= 3.182`

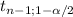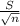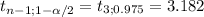
For population 1 (Wages)

n₁= 4; X[bar]₁= 13.74; S₁= 1.95

13.74±3.182*
`(1.95)/(√(4) )`]

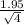[10.65; 16.85]

Using a 95% confidence level you'd expect that the interval [10.65; 16.85] contains the population mean of the wages of U.S. employees.

For population 2 (Education)

n₂= 4; X[bar]₂= 12.25; S₂= 0.50

12.25±3.182*
`(0.50)/(√(4) )`]

[14.45; 13.05]

Using a 95% confidence level you'd expect that the interval [14.45; 13.05] contains the value of the average education of U.S. employees.

ii.

To estimate Rho (the population correlation coefficient) you have to use the following formula:

`r= \frac{sumX_1X_2-((sumX_1)(sumX_2))/(n) }{\sqrt{[sumX_1^2-((sumX_1)^2)/(n_1) ][sumX_2^2-((sumX_2)^2)/(n_2) ]} }`

∑X₁= 54.96; ∑X₁²= 766.57; ∑X₂= 49; ∑X₂²= 601; ∑X₁X₂= 671.88

`r= \frac{671.88-(54.96*49)/(4) }{\sqrt{[766.57-((54.96)^2)/(4) ][601-((49)^2)/(4) ]} }`

r= -0.47

iii.

To estimate the regression using Y: wage and X: education you have to estimate the intercept and the slope of the equation:

Estimate of the slope "b"

`b= (sumXY-((sumX)(sumY))/(n) )/([sumX^2-((sumX)^2)/(n) ]) = (671.88-(54.96*49)/(4) )/(601-(49^2)/(4) ) = -1.84`

Estimate of the intercept "a"

`a= Y[bar] - b*X[bar]= 13.74 - (-1.84)*12.25= 36.28`

The estimated regression equation is ^Y= 36.28 - 1.84X

iv.

You have to estimate the value of the wages ^Y given X= 15years of education. To do so you have to replace the value of X in the estimated regression equation:

^Y= 36.28 - 1.84*15= 8.68

For a level of education of 15 years, the estimated wage is 8.68

v. The value of the coefficient of determination is R²= 0.22

This means that 22% of the variability of the average wages of U.S. employees is explained by the years of education. For the estimated model ^Y= 36.28 - 1.84X.

I hope this helps!