Question

Keita left camp three days ago on a journey into the jungle. The three days of his journey can be described by displacement (distance and direction) vectors ​d​1​​, ​d​2​​, and ​d​3.

​d​1​​=(7,8)

​d​2​​=(6,2)

​d​3​​=(2,9) (Distances are given in kilometers, km.)

How far is Keita from camp at the end of day three?(Round your final answer to the nearest tenth.) 24.2km

What direction is Keita from camp at the end of day three?

Answer 1

Keita is 24.2 km far from the camp at the end of day three

Thus Keita is at 51.71° to the x-axis direction

Step-by-step explanation:

Given that:

the displacement vector for Keita's Journey are :

​d​1​​=(7,8)

​d​2​​=(6,2)

​d​3​​=(2,9)

Then the final displacement
`d\limits ^(\to) = (d_1\limits ^(\to) + d_2\limits ^(\to) + d_3\limits ^(\to) )`

`d\limits ^(\to) = (7+6+2, \ \ 8+2+9 )`

`d\limits ^(\to) = (15, \ \ 19)`

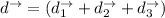
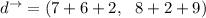
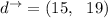
How far is Keita from camp at the end of day three?

i.e

`|d| = √((15)^2+(19)^2)`

`|d| = √(225+361)`

`|d| = √(586)`

`\mathbfd`

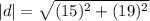
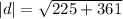
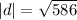
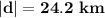
Keita is 24.2 km far from the camp at the end of day three

What direction is Keita from camp at the end of day three?

From the diagram attached below, Taking the tangent of the coordinates; we have:

tan θ =
`(y)/(x)`

tan θ =
`(19)/(15)`

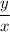
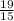
tan θ = 1.2667

θ = tan⁻¹ (1.2667)

θ = 51.71°

Thus Keita is at 51.71° to the x-axis direction