Answer:
Keita is 24.2 km far from the camp at the end of day three
Thus Keita is at 51.71° to the x-axis direction
Step-by-step explanation:
Given that:
the displacement vector for Keita's Journey are :
d1=(7,8)
d2=(6,2)
d3=(2,9)
Then the final displacement

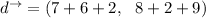
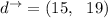
How far is Keita from camp at the end of day three?
i.e
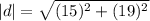
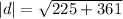

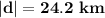
Keita is 24.2 km far from the camp at the end of day three
What direction is Keita from camp at the end of day three?
From the diagram attached below, Taking the tangent of the coordinates; we have:
tan θ =
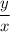
tan θ =
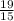
tan θ = 1.2667
θ = tan⁻¹ (1.2667)
θ = 51.71°
Thus Keita is at 51.71° to the x-axis direction