Question

The Salk polio vaccine experiment in 1954 focused on the effectiveness of the vaccine in combating paralytic polio. Because it was felt that without a control group of children there would be no sound basis for evaluating the efficacy of the Salk vaccine, the vaccine was administered to one group, and a placebo (visually identical to the vaccine but known to have no effect) was administered to second group. For ethical reasons, and because it was suspected that knowledge of the vaccine administration would effect subsequent diagnoses, the experiment was conducted in a double blind fashion. That is, neither the subjects nor the administrators knew who received the vaccine and who received the placebo. The actual data for this experiment are as follows:

Placebo Group: n = 201, 299 : 110 cases of polio observed
Vaccine Group: n = 200, 745 : 33 cases of polio observed

(a) Use a hypothesis-testing procedure to determine whether the proportion of children in the two groups who contracted paralytic polio is statistically different. Use a probability of a type I error equal to 0.05.

(b) Repeat part (a) using a probability of a type I error equal to 0.01.

(c) Compare your conclusions from parts (a) and (b) and explain why they are the same or different.

Answer 1

Explanation:

Hello!

The variables of interest are:

X₁: Number of cases of polio observed in kids that received the placebo vaccine.

n₁= 201299 total children studied

x₁= 110 cases observed

X₂: Number of cases of polio observed in kids that received the experimental vaccine.

n₂= 200745 total children studied

x₂= 33 cases observed

These two variables have a binomial distribution. The parameters of interest, the ones to compare, are the population proportions: p₁ vs p₂

You have to test if the population proportions of children who contracted polio in both groups are different: p₂ ≠ p₁

a)

H₀: p₂ = p₁

H₁: p₂ ≠ p₁

α: 0.05

`Z= \frac{(p'_2-p'_1)-(p_2-p_1)}{\sqrt{p'[(1)/(n_1) +(1)/(n_2) ]} }`

Sample proportion placebo p'₁= x₁/n₁= 110/201299= 0.0005

Sample proportion vaccine p'₂= x₂/n₂= 33/200745= 0.0002

Pooled sample proportion p'= (x₁+x₂)/(n₁+n₂)= (110+33)/(201299+200745)= 0.0004

`Z_(H_0)= \frac{(0.0002-0.0005)-0}{\sqrt{0.0004[(1)/(201299) +(1)/(200745) ]} }= -4.76`

This test is two-tailed, using the critical value approach, you have to determine two critical values:

`Z_(\alpha/2)= Z_(0.025)= -1.96`

`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

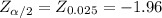
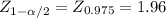
Then if
`Z_(H_0)` ≤ -1.96 or if
`Z_(H_0)` ≥ 1.96, the decision is to reject the null hypothesis.

If -1.96 <
`Z_(H_0)` < 1.96, the decision is to not reject the null hypothesis.

⇒
`Z_(H_0)`= -4.76, the decision is to reject the null hypothesis.

b)

H₀: p₂ = p₁

H₁: p₂ ≠ p₁

α: 0.01

`Z= \frac{(p'_2-p'_1)-(p_2-p_1)}{\sqrt{p'[(1)/(n_1) +(1)/(n_2) ]} }`

The value of
`Z_(H_0)`= -4.76 doesn't change, since we are working with the same samples.

The only thing that changes alongside with the level of significance is the rejection region:

`Z_(\alpha /2)= Z_(0.005)= -2.576`

`Z_(1-\alpha /2)= Z_(0.995)= 2.576`

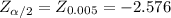
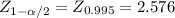
Then if
`Z_(H_0)` ≤ -2.576or if
`Z_(H_0)` ≥ 2.576, the decision is to reject the null hypothesis.

If -2.576<
`Z_(H_0)` < 2.576, the decision is to not reject the null hypothesis.

⇒
`Z_(H_0)`= -4.76, the decision is to reject the null hypothesis.

c)

Remember the level of significance (probability of committing type I error) is the probability of rejecting a true null hypothesis. This means that the smaller this value is, the fewer chances you have of discarding the true null hypothesis. But as you know, you cannot just reduce this value to zero because, the smaller α is, the bigger β (probability of committing type II error) becomes.

Rejecting the null hypothesis using different values of α means that there is a high chance that you reached a correct decision (rejecting a false null hypothesis)

I hope this helps!