Question

Elena wonders how much water it would take to fill her cup. She drops her pencil in her cup and notices that it just fits diagonally. (See the diagram.) The pencil is 17 cm long and the cup is 15 cm tall. How much water can the cup hold? Explain or show your reasoning.

Answer 1

The cup can hold 240π cubic centimeters of water.

Explanation:

Let's assume the cup is a cylinder. The pencil length is simulates a diagonal (hypothenuse), which forms a right triangle with the height of the cylinder and the diameter at the bottom. So, we apply Pythagorean's Theorem.

`17^(2) =15^(2) + d^(2)`

Solving for
`d`, we have

`289 - 225 = d^(2) \\d=√(64) \\ d=8`

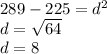
Therefore, the diameter of the cylinder is 8 centimeres, which means its radius is 4 centimeters by definition.

The volume of a cylinder is defined as

`V= \pi r^(2) h`

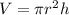
Where
`r` is the radius and
`h` is the height. Replacing values, we have

`V= \pi * 4^(2) * 15 =\pi * 16 * 15\\V=240\pi \ cm^(3)`

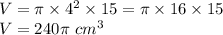
Therefore, the cup can hold 240π cubic centimeters of water.