Question

You are given the market demand function Q=2800-1000p, and that each duopoly firm's marginal cost is $0.07 per unit, which implies the cost function: C(qi)=.07qi, assuming no fixed costs for i= 1,2. The Cournot equilibrium quantities are: q1= _____; and q2 _____.

Answer 1

q1 = 910

q2 = 910

Step-by-step explanation:

Given:

Q = 2800 - 1000p

Marginal cost = $0.07 per unit

Q = 2800 - 1000p

`p = (2800 - Q)/(1000)`

`p = (2800- q_1 - q_2)/(1000)`

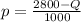
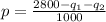
Let's calculate profit of firm 1:

TR = p1 q1

`= (2800 q_1 - q_1^2 - q_1 q_2)/(1000)`

`MR = (2800 - 2q_1 - q_2)/(1000)`

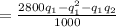
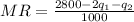
MR = MC = 0.07

`(2800 - 2q_1 - q_2)/(1000) = 0.07`

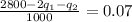
Cross multiplying:

2800 - 2q₁ - q₂ = 70

2800 - 2q₁ = 70 + q₂

2800 - 70 - 2q₁ = q₂

2730 - 2q₁ = q₂...............(1)

Let's calculate profit of firm 2:

TR = p₁ q₂

`= (2800 q_2 - q_1 - q_2^2)/(1000)`

`(2800 - q_1 - 2q_2)/(1000) = MR`

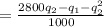
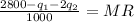
MR = MC = 0.07

`(2800 - q_1 - 2q_2)/(1000) = 0.07`

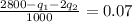
Cross multiplying:

2800 - q₁ - 2q₂ = 70

2800 - 2q₂ = 70 + q₁

2800 - 70 - 2q₂ = q₁

2730 - 2q₂ = q₁................... (2)

Substitute 2730 - 2q₂ for q₁ in (1)...

Thus:

2730 - 2q₁ = q₂

2730 - 2(2730 - 2q₂) = q₂

2730 - 5460 + 4q₂ = q₂

-2730 + 4q₂ = q₂

-2730 = q₂ - 4q₂

-2730 = - 3q₂

q₂ = -2730/-3

q₂ = 910

Substituting 910 for q₂ in (2):

2730 - 2q₂ = q₁

2730 - 2(910)= q₁

2730 - 1820 = q₁

910 = q₁

q₁ = 910

The Cournot equilibrium quantities are: q₁= 910; and q₂ = 910