Answer:
The measure of the side AB is 26 cm.
Explanation:
The question is:
In a triangle ABC the hypotenuse BC measures 30 cm, it is known that the angle of the opposite angle to the side AB, measures 60°, therefore it is concluded that as side AB the triangle measures ?
Solution:
Consider the triangle ABC.
The side BC is defined as a hypotenuse. This implies that the triangle ABC is a right angled triangle.
The angle A measures 90° and the angle C measures 60°.
The hypotenuse length is 30 cm.
According to the trigonometric identities for right angled triangle:
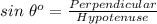
Compute the length of side AB as follows:
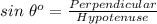
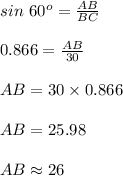
Thus, the measure of the side AB is 26 cm.