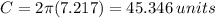Question

The area of the sector formed by the 110 degree central angle is 50 units squared. What is the circumference of the circle

Answer 1

The circumference of the circle is
`C=45.346 \:units`.

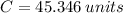Explanation:

A sector is the part of a circle enclosed by two radii of a circle and their intercepted arc. A pie-shaped part of a circle.

The area of a circle is given by
`A_(circle)=\pi r^2`

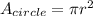
The formula used to calculate the area of a sector of a circle is:

`A_(sector)=(central \:angle)/(360) \cdot {Area \:of \:whole \:circle}\\\\A_(sector)=(\theta)/(360) \cdot \pi r^2`

The circumference of a circle is the distance around the outside of the circle and its given by

`C=2\pi r`

We know the central angle
`\theta` = 110º and the area of the sector 50 units squared.

First, we use the formula to calculate the area of a sector to find the radius.

`50=(110)/(360) \cdot \pi r^2\\\\(110)/(360)\pi r^2=50\\\\(11\pi )/(36)r^2=50\\\\11\pi r^2=1800\\\\r^2=(1800)/(11\pi )\\\\\mathrm{For\:}x^2=f\left(a\right)\mathrm{\:the\:solutions\:are\:}x=√(f\left(a\right)),\:\:-√(f\left(a\right))\\\\r=\sqrt{(1800)/(11\pi )},\:r=-\sqrt{(1800)/(11\pi )}`

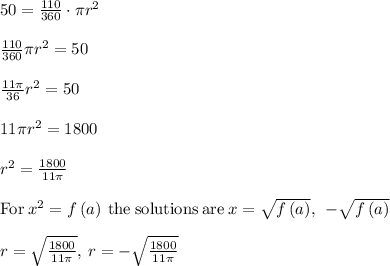
The radius can't be negative. Therefore,

`r=\sqrt{(1800)/(11\pi )}\approx 7.217 \:units`

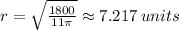
Next, we apply the formula for the circumference of a circle.

`C=2\pi (7.217)=45.346 \:units`