Question

A small tank has a cylindrical shape. It has a radius of 15 inches and a height of 48 inches. A can of spray paint will cover 720 square inches. How many cans of paint must be bought to completely cover the tank with one coat of paint?

HELP FAST WILL GIVE LOTS OF POINTS

Answer 1

c) 9

Explanation:

`\textsf{Surface area of a cylinder}=2\pi r^2+2\pi rh`

(where r is the radius and h is the height)

Given:

• r = 15 in
• h = 48 in

Substitute given values into the equation to find the surface area:

`\begin{aligned}\implies \textsf{Surface area} & =2\pi (15)^2+2\pi (15)(48)\\ & =1890 \pi\: \sf in^2\end{aligned}`

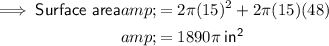
To calculate the number of cans of paint to be bought, divide the surface area by the area one can of paint will cover:

`\implies (1890 \pi)/(720)=8.246680716...`

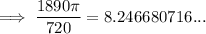
We need to round this number up, as rounding down will mean we will not have quite enough paint to cover the surface area of the cylinder.

Therefore, the numnber of cans of paint that must be bought to completely cover the tank with one coat of paint is 9.