Question

1. Suppose you have a dark closet containing seven blue shirts, five yellow shirts, and eight

white shirts. You pick two shirts at random from the closet. Find each probability.
a. P(blue then yellow) with replacing b. P(blue then yellow) without replacing
C. P(yellow then yellow) with replacing d. Plyellow then yellow) without replacing
e. P(yellow then white) with replacing f. P(yellow then white) without replacing
g. P(blue then blue) with replacing h. P(blue then blue) without replacing

Answer 1

A) P = 0.0875

B) P = 0.092

C) P = 0.0625

D) P = 0.053

E) P = 0.100

F) P = 0.105

G) P = 0.1225

H) P = 0.1105

Explanation:

A) The probability of picking a blue shirt is
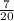`(7)/(20)`. After replacing it, there are still 20 shirts, so the probability of picking a yellow shirt is
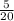`(5)/(20)`. As the blue shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

B) The probability of picking a blue shirt is
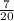`(7)/(20)`. Without replacing it, there are 19 shirts, so the probability of picking a yellow shirt is
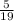`(5)/(19)`. As the blue shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

C) The probability of picking a yellow shirt is
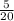`(5)/(20)`. After replacing it, there are still 20 shirts, so the probability of picking a yellow shirt is
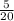`(5)/(20)`. As the yellow shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

D) The probability of picking a yellow shirt is
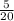`(5)/(20)`. Without replacing it, there are 19 shirts, so the probability of picking a yellow shirt is
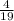`(4)/(19)` (as there is one less yellow shirt). As the yellow shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

E) The probability of picking a yellow shirt is
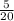`(5)/(20)`. After replacing it, there are still 20 shirts, so the probability of picking a white shirt is
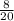`(8)/(20)`. As the yellow shirt AND the white shirt must be picked then you multiply the two probabilities together.

F) The probability of picking a yellow shirt is
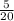`(5)/(20)`. Without replacing it, there are 19 shirts, so the probability of picking a white shirt is
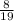`(8)/(19)`. As the yellow shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

G) The probability of picking a blue shirt is
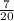`(7)/(20)`. After replacing it, there are still 20 shirts, so the probability of picking a blue shirt is
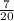`(7)/(20)`. As the blue shirt AND the yellow shirt must be picked then you multiply the two probabilities together.

H) The probability of picking a blue shirt is
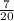`(7)/(20)`. Without replacing it, there are 19 shirts, so the probability of picking a blue shirt is
`(6)/(19)` (as there is one less blue shirt). As the blue shirt AND the blue shirt must be picked then you multiply the two probabilities together.