Question

For a standard normal distribution, find the approximate value of P(-0.78 sz51 16). Use the portion of the standard normal

table below to help answer the question

Answer 1

c.66%

edg

Explanation:

Answer 2

The value of P (-0.78 < z < 1.16) is 0.6593.

Explanation:

A random variable
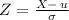`Z=(X-\,u)/(\sigma)` is said to follow a standard normal distribution if
`X\sim N(\mu,\ \sigma^(2))`. The random variable Z has mean 0 and variance 1.

The probability expression is:

P (-0.78 < z < 1.16)

Use the standard normal table to compute the probability value as follows:

`P (-0.78 <z< 1.16)=P(z< 1.16)-P(z< -0.78)`

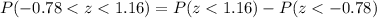
`=P(z<1.16)-[1-P(z<0.78)]\\=P(z<1.16)-1+P(z<0.78)\\=0.87698-1+0.78230\\=0.65928\\\approx 0.6593`

Thus, the value of P (-0.78 < z < 1.16) is 0.6593.