Question

What are the explicit equation and domain for an arithmetic sequence with a first term of 8 and a second term of 5?

A. an = 8 − 5(n − 1); all integers where n ≥ 1
B. an = 8 − 5(n − 1); all integers where n ≥ 0
C. an = 8 − 3(n − 1); all integers where n ≥ 1
D. an = 8 − 3(n − 1); all integers where n ≥ 0

Answer 1

The correct answer is:

C.
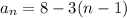`a_n=8-3(n-1)`; all integers where n ≥ 1.

Explanation:

In general, this is the standard explicit equation of an arithmetic sequence whose first term is
`a_1` and common difference (It is the difference between the terms) is
`d`.

`a_n=a_1+d(n-1)`

If our arithmetic sequence has the first term 8 and second 5, thus the difference is -3.

The standard explicit equation is
`a_n=8-3(n-1)`.

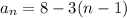The domain in arithmetic sequence is always all integers where
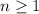`n\geq 1`. There's no such thing as the negative fifth term or the 0.4th term of a sequence.