Question

The endpoints of a diameter of a circle are located at(-3,6) and (7,-12). What is the equation of the circle? A. (×+2)2+(y+3)2=square 106 B. (X-4)2+(y+6)2

Answer 1

`(x-2)^2+(y+3)^2=106`.

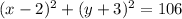Explanation:

It is given that the endpoints of a diameter of a circle are located at(-3,6) and (7,-12). It means center of the circle is the midpoint of (-3,6) and (7,-12).

`Center=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Center=\left((-3+7)/(2),(6-12)/(2)\right)`

`Center=\left(2,-3\right)`

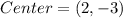
The center of the circle is (2,-3).

Radius is the distance between center and the endpoint of diameter. So, radius is equal to the distance between (2,-3) and (-3,6).

`r=√((x_2-x_1)^2+(y_2-y_1)^2)`

`r=√((-3-2)^2+(6-(-3))^2)`

`r=√(25+81)`

`r=√(106)`

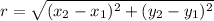
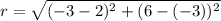
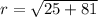
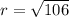
The standard form of the circle is

`(x-h)^2+(y-k)^2=r^2`

where, (h,k) is center and r is radius.

Substitute h=2, k=-3 and
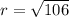`r=√(106)` in the above equation.

`(x-2)^2+(y-(-3))^2=(√(106))^2`

`(x-2)^2+(y+3)^2=106`

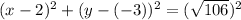
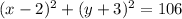
Therefore, the required equation of circle is
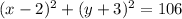`(x-2)^2+(y+3)^2=106`.