Answer:
t = 1.57 sec
distance, d = 98.65 mm
Explanation:
Given an angle of 540°
At 6 revolutions per second, which is the angular velocity.
Radius, r = 10 mm
We are asked to find the time and the distance.
To find the time, let's use the formula:
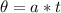
Where
 = angle in radians.
= angle in radians.
Converting 540° to radians, we have:
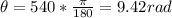
Therefore, from the formula, let's find t.
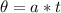
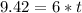
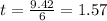
time = 1.57
To find the distance, we have:
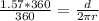
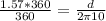
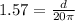
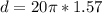
d = 98.65 mm
Therefore, the time is 1.57 seconds and the distance is 98.65 mm