Let a be the first term in the sequence, and d the common difference between consecutive terms. If aₙ denotes the n-th term in the sequence, then
a₁ = a
a₂ = a₁ + d = a + d
a₃ = a₂ + d = a + 2d
a₄ = a₃ + d = a + 3d
and so on, up to the n-th term
aₙ = a + (n - 1) d
The sum of the first 10 terms is 100, and so
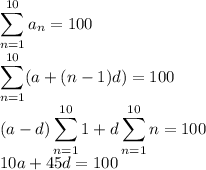
where we use the well-known sum formulas,
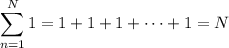
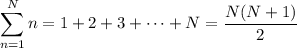
The sum of the next 10 terms is 300, so
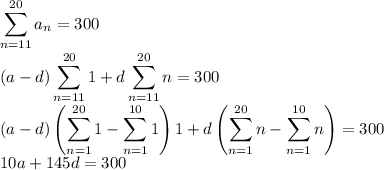
Solve for a and d. Eliminating a gives
(10a + 145d) - (10a + 45d) = 300 - 100
100d = 200
d = 2
and solving for a gives
10a + 145×2 = 300
10a = 10
a = 1
So, the given sequence is simply the sequence of positive odd integers,
{1, 3, 5, 7, 9, …}
given recursively by the relation
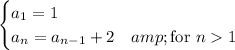
and explicitly by
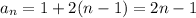
for n ≥ 1.