Question

What is the area of the square that shares a side with the third side of the triangle?​

Answer 1

Complete question:

Two sides of a right triangle measure 7 units and 3 units. What is the area of the square that shares a side with the third side of the triangle?

Answer:

`C = (√(58)) ^2`

Explanation:

Given:

A = 7 units

B = 3 units

To find the length of the third side, let's use Pythagoras theorem.

C² = A² + B²

Substituting figures, we have:

C² = 7² + 3²

C² = 49 + 9

C² = 58

`C = √(58)`

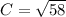
The length of the third side, C is
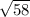`√(58)` units.

Since the length of the third side is
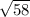`√(58)` units, the area of the square that shares a side with the third side of the triangle would be C².

Therefore, C² =
`√(58)^2`