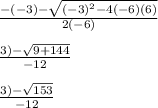Question

6- 6x^2- 3x = 0 solve

Answer 1

The solutions are
`x=(3)+√(153) )/(-12)`,
`x=(3)-√(153) )/(-12)`

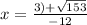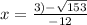
If you need to have them in a decimal form rounded to 3 decimals, the answers would be
`x=-1.281`,
`x=0.781`

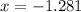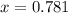
Explanation:

We are given the equation
`6-6x^2-3x=0`

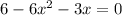
The first thing that can be done is to rearrange the terms so that they are in descending order of power. This makes it easier to work with

This gives us
`-6x^2-3x+6=0`

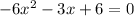
To find the solutions to this equation, we can use the quadratic formula, which will tell us that the solutions are equal to
`(-b+√(b^2-4ac) )/(2a) ,(-b-√(b^2-4ac) )/(2a)`

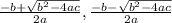
From our equation, we can gather that
`a=-6, b=-3, c=6`

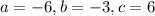
Now that we have our variables, we can plug them into the quadratic formula to get our solutions.

`(-(-3)+√((-3)^2-4(-6)(6)) )/(2(-6))\\\\(3)+√(9+144) )/(-12)\\\\(3)+√(153) )/(-12)`

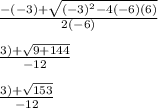
And now for our second equation

`(-(-3)-√((-3)^2-4(-6)(6)) )/(2(-6))\\\\(3)-√(9+144) )/(-12)\\\\(3)-√(153) )/(-12)`