Question

Suppose you want to estimate the proportion of cars that are sport utility vehicles (SUVs) being driven in Kansas City, Missouri, at rush hour by standing on the corner of I-70 and I-470 and counting SUVs. You believe the figure is no higher than 0.40. If you want the error of the confidence interval to be no greater than .03, how many cars should you randomly sample? Use a 90% level of confidence.

Answer 1

The sample size 'n' = 721

Number of cars 'n' = 721

Explanation:

Explanation:-

Given Population proportion 'p' = 0.40

Given Margin of error = 0.03

90% of level of significance

`Z_{(\alpha )/(2) } = 1.645`

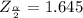
The Margin of error is determined by

`M.E = \frac{Z_{(\alpha )/(2) S.D} }{√(n) }`

`0.03 = (1.645 X √(0.40(1-0.40) ) )/(√(n) )`

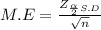
on calculation , we get

0.03√n = 0.8058

`√(n) = (0.8058)/(0.03) = 26.86`

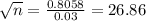
squaring on both sides , we get

n = 721.45≅721

conclusion:-

The sample size 'n' = 721

Number of cars 'n' = 721