Question

The polynomial p(x)=7^3-7x-6 has a known factor of (x+1) rewrite p(x) as a product of linear functions

Answer 1

`p(x)=(x+1)(x+2)(x-3)`.

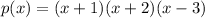Explanation:

Note: The given function is not correct.

Consider the given polynomial is

`p(x)=x^3-7x-6`

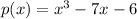
It is given that (x+1) is a factor of given function.

Using synthetic division, divide P(x) by (x+1) as shown below.

-1 | 1 0 -7 -6

| -1 1 6

--------------------------------------

1 -1 -6 0

--------------------------------------

Bottom line represents the coefficients of quotient except the last element because it is remainder. So, the given function can be written as

`p(x)=(x+1)(x^2-x-6)`

`p(x)=(x+1)(x^2-3x+2x-6)`

`p(x)=(x+1)(x(x-3)+2(x-3))`

`p(x)=(x+1)(x+2)(x-3)`

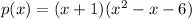
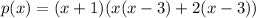
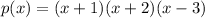
Therefore, the function as a product of linear functions is
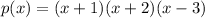`p(x)=(x+1)(x+2)(x-3)`.