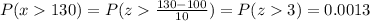Question

1) On a standardized aptitude test, scores are normally distributed with a mean of 100 and a standard deviation of 10. Find the PERCENT of scores that are:

A) Between 90 and 100.


B) Over 110


C) Between 80 and 120


D) Less than 80


E) Between 70 and 100


F) More than 130

Answer 1

A) 34.13%

B) 15.87%

C) 95.44%

D) 97.72%

E) 49.87%

F) 0.13%

Explanation:

To find the percent of scores that are between 90 and 100, we need to standardize 90 and 100 using the following equation:

`z=(x-m)/(s)`

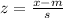
Where m is the mean and s is the standard deviation. Then, 90 and 100 are equal to:

`z=(90-100)/(10)=-1\\ z=(100-100)/(10)=0`

So, the percent of scores that are between 90 and 100 can be calculated using the normal standard table as:

P( 90 < x < 100) = P(-1 < z < 0) = P(z < 0) - P(z < -1)

= 0.5 - 0.1587 = 0.3413

It means that the PERCENT of scores that are between 90 and 100 is 34.13%

At the same way, we can calculated the percentages of B, C, D, E and F as:

B) Over 110

`P( x > 110 ) = P( z>(110-100)/(10))=P(z>1) = 0.1587`

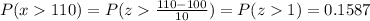
C) Between 80 and 120

`P( 80<x< 110 ) = P( (80-100)/(10) <z>(120-100)/(10))=P(-2<z<2)\\P(-2<z<2)=P(z<2) - P(z<-2) = 0.9772 - 0.0228 = 0.9544`

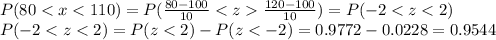
D) less than 80

`P( x < 80 ) = P( z<(80-100)/(10))=P(z<-2) = 0.9772`

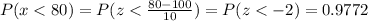
E) Between 70 and 100

`P( 70<x< 100 ) = P( (70-100)/(10) <z>(100-100)/(10))=P(-3<z<0)\\P(-3<z<0)=P(z<0) - P(z<-3) = 0.5 - 0.0013 = 0.4987`

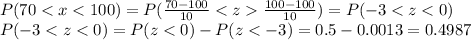
F) More than 130

`P( x > 130 ) = P( z>(130-100)/(10))=P(z>3) = 0.0013`