Question

1. Let f(x) be a polynomial such that f(0)=4, f(1)=5, and f(2)=10. Find the remainder when f(x) is divided by x(x-1)(x-2)

2. Find a polynomial f(x) of degree 5 such that both of these properties hold:

f(x) is divisible by x^3

f(x)+2 is divisible by (x+1)^3

Answer 1

1. The remainder is 2·x² - x + 4

2. The polynomial is 12·x⁵ + 30·x⁴ + 20·x³

Explanation:

Here we have that the polynomial is to be divided by x(x-1)(x-2) with a remainder, hence the polynomial should be at least degree 3

Therefore

`(f(x))/(x(x-1)(x-2)) = g(x) + (ax^2+bx+c)/(x(x-1)(x-2))`

`(f(x) * x(x-1)(x-2))/(x(x-1)(x-2)) = g(x) x(x-1)(x-2) + ax^2+bx+c`

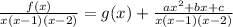
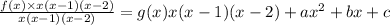
Therefore, f(x) = g(x)·x·(x-1)·(x-2)+a·x² + b·x + c

We substitute the values of x and f(x) to get

f(0) = c = 4

f(1) = a + b + 4 = 5 which gives a + b = 1.......................(1)

f(2) = 4·a + 2·b + 4 = 10 which gives 4·a + 2·b = 6----(2)

Multiplying equation (1) by 2 and subtracting it from equation (2), we get

2·a = 4

a = 2 ∴ b = 1 - 2 = -1

Hence, f(x) divided by x·(x-1)·(x-2), the remainder = 2·x² - x + 4

2. Here we have

f(x) is divisible by x³ gives

f(x) = x³(ex² + fx + g) = e·x⁵ + f·x⁴ + g·x³

and f(x) + 2 = (x + 1)³(a·x² + b·x +c) = a·x⁵ + (3·a+b)·x⁴ + (3·a+3·b+c)·x³ + (a+3·b+3·c)·x² + (b+3·c)·x + c

f(x) = (x + 1)³(a·x² + b·x +c) = a·x⁵ + (3·a+b)·x⁴ + (3·a+3·b+c)·x³ + (a+3·b+3·c)·x² + (b+3·c)·x + c - 2

Therefore, the coefficients of x², x and the constants are equal to 0

We have

a+3·b+3·c = 0

b+3·c = 0

c - 2 = 0

Hence, c = 2, b = -6, a = 12

Therefore the polynomial = 12·a⁵ + 30·x⁴ + 20·x³.