Question

A total charge of –6.50 µC is uniformly distributed within a sphere that has a radius of 0.150 m. What is the magnitude and direction of the electric field at 0.300 m from the surface of the sphere? A) 2.89 × 105 N/C, radially inward B) 6.49 × 105 N/C, radially outward C) 4.69 × 105 N/C, radially inward D) 9.38 × 105 N/C, radially outward E) 1.30 × 106 N/C, radially inward

Answer 1

A) 2.89 × 105 N/C, radially inward

Step-by-step explanation:

The magnitude of the electric field generated by a charged sphere is given by the following formula:

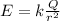`E=k(Q)/(r^2)` ( 1 )

k: Coulomb's constant = 8.98*10^9 Nm^2/C^2

Q: charge of the sphere = -6.50*10^-6 C

r: distance from the center of the sphere to the point in which E is calculated

r = 0.150m + 0.300m = 0.450 m

You replace the values of Q and r in the equation (1):

`E=(8.98*10^9Nm^2/C^2)(6.50*10^(-6)C)/((0.450m)^2)=288246.91(N)/(C)\\\\E\approx2.89*10^5(N)/(C)`

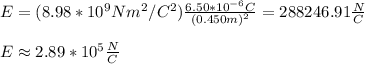
The electric field points radially inward because the charge is negative.

hence, the answer is:

A) 2.89 × 105 N/C, radially inward