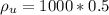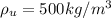Answer:
The density is
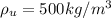
Step-by-step explanation:
From the question we are told that
The weight in air is
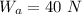
The weight in water is
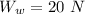
The weight in a unknown liquid is

Now according to Archimedes principle the weight of the object in water is mathematically represented as
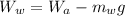
Where
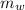 is he mass of the water displaced
is he mass of the water displaced
substituting value
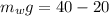
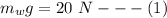
Now according to Archimedes principle the weight of the object in unknown is mathematically represented as
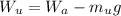
Where
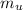 is he mass of the unknown liquid displaced
is he mass of the unknown liquid displaced
substituting value
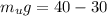
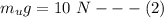
dividing equation 2 by equation 1
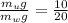
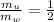
=>
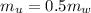
Now since the volume of water and liquid displaced are the same then
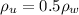
This because
So if volume is constant
mass = constant * density
Where
 is the density of the liquid
is the density of the liquid
and
 is the density of water which is a constant with a value
is the density of water which is a constant with a value
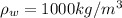
So