Question

1.Mr. Bowen’s test is normally distributed with a mean of 75 and a standard deviation of 3 points.

Answer 1

2.28%

Explanation:

Mr. bowens test is normally distributed with a mean (μ) of 75 and a standard deviation (σ) of 3 points.

The z score is used in probability to show how many standard deviation is a raw score below or above the mean. The formula for the z score (z) is given by:

`z=(x-\mu)/(\sigma)`

For a raw score (x) of 81 points, the z score can be calculated by:

`z=(x-\mu)/(\sigma)=(81-75)/(3)=2`

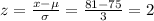
Therefore from the normal probability distribution table, the probability that a randomly selected score is greater than 81 can be given as:

P(x > 81) = P(z > 2) = 1 - P(z < 2) = 1 - 0.9772 = 0.0228 = 2.28%