Answer:
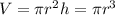
And we can solve for the radius:
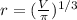
And replacing we got:
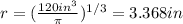
And the volume for a sphere is given by:
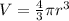
And replacing we got:
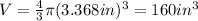
And the best option for this case is:
C 160 cubic inches
Explanation:
For this case we know that the volume for the cylinder is 120 in^3. We know that the radius of this cylinder is equal to the height so then the volume can be founded with this formula:
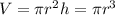
And we can solve for the radius:
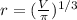
And replacing we got:
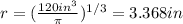
And the volume for a sphere is given by:
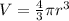
And replacing we got:
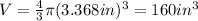
And the best option for this case is:
C 160 cubic inches