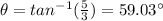Question

At each corner of a square of side l there are point charges of magnitude Q, 2Q, 3Q, and 4Q.What is the magnitude and direction of the force on the charge of 2Q?

Answer 1

`F_T=6k(Q^2)/(L)\hat{i}+10k(Q^2)/(L)\hat{j}=2k(Q^2)/(L)[3\hat{i}+5\hat{j}]`

`|F_T|=2√(34)k(Q^2)/(L)`

`\theta=tan^(-1)((5)/(3))=59.03\°`

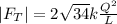
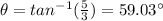
Step-by-step explanation:

I attached an image below with the scheme of the system:

The total force on the charge 2Q is the sum of the contribution of the forces between 2Q and the other charges:

`F_T=F_Q+F_(3Q)+F_(4Q)\\\\F_T=k((Q)(2Q))/(R_1)\hat{i}+k((3Q)(2Q))/(R_2)\hat{j}+k((4Q)(2Q))/(R_3)[cos\theta \hat{i}+sin\theta \hat{j}]`

the distances R1, R2 and R3, for a square arrangement is:

R1 = L

R2 = L

R3 = (√2)L

θ = 45°

`F_T=k(2Q^2)/(L)\hat{i}+k(6Q^2)/(L)\hat{j}+k(8Q^2)/(√(2)L)[cos(45\°)\hat{i}+sin(45\°)\hat{j}]\\\\F_T=k(2Q^2)/(L)\hat{i}+k(6Q^2)/(L)\hat{j}+k(8Q^2)/(√(2)L)[(√(2))/(2)\hat{i}+(√(2))/(2)\hat{j}]\\\\F_T=6k(Q^2)/(L)\hat{i}+10k(Q^2)/(L)\hat{j}=2k(Q^2)/(L)[3\hat{i}+5\hat{j}]`

and the magnitude is:

`|F_T|=2k(Q^2)/(L)√(3^2+5^2)=2√(34)k(Q^2)/(L)`

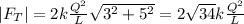
the direction is:

`\theta=tan^(-1)((5)/(3))=59.03\°`