Question

Write an approximate equation of the line of best fit, then predict the average temperature.

Answer 1

`\textsf{\sf(a)} \quad y=-\frac54x+(205)/(2)`

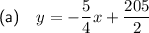
(b) $46.25

Explanation:

When adding a line of best fit, ensure that the number of points above and below the line is about equal.

See attachment for line of best fit.

Part (a)

From inspection of the graph, two points on the line are (10, 90) and (50, 40). Therefore,

`\textsf{let}\:(x_1,y_1)=(10,90)`

`\textsf{let}\:(x_2,y_2)=(50,40)`

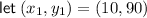
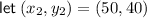
Calculating the slope of the line:

`\textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(40-90)/(50-10)=-\frac54`

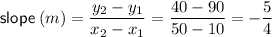
Using the point-slope form of linear equation:
`y-y_1=m(x-x_1)`

(where m is the slope and (x₁, y₁) is a point on the line)

`\implies y-90=-\frac54(x-10)`

`\implies y-90=-\frac54x+(25)/(2)`

`\implies y=-\frac54x+(205)/(2)`

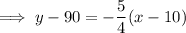
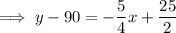
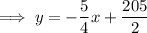
(where x is the average monthly temperature in °F and y is the monthly heating costs in dollars)

Part (b)

Substitute x = 45 into the equation found in part (a):

`\implies -\frac54(45)+(205)/(2)=46.25`

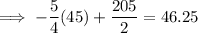
Therefore, the monthly heating cost for a month with an average temperature of 45 °F is approximately $46.25