Question

A circle is cut into congruent sections and arranged to form a figure that approximates a parallelogram. Find the approximate height of the figure when its area is 42.25π square centimeters.

Answer 1

Approximate height of the figure is 6.5 cm.

Explanation:

Area of a parallelogram = base × height

Area of a circle =
`\pi r^(2)`

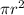
where r is the radius of the circle.

From the question, a circle was cut to approximate a parallelogram. Thus:

area of the parallelogram = area of the circle =
`\pi r^(2)`

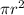
Given that area of the circle is 42.25
`\pi` square centimetres, which is the area of the figure, then;

42.25
`\pi` =
`\pi r^(2)`

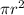
⇒ 42.25 =
`r^(2)`

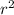
Find the square root of both sides, we have;

r =
`√(42.25)`

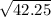
r = 6.5

The radius of the circle is 6.5 cm.

From the figure, the radius of the circle is approximately equal to the height of the parallelogram. So that the height of the parallelogram is 6.5 cm.