Question

What is the energy of an electromagnetic wave that has a wavelength of 7.0×10^-12 m? Use the equation E- Intion hc

Answer 1

Assume that this wavelength is measured in vacuum. The energy on each photon of this wave would be approximately
`2.8 * 10^(-14)\; \rm J`.

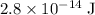Step-by-step explanation:

The Planck-Einstein Relation relates the energy
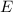`E` of a photon to its frequency
`f`:

`E = h \, f`,

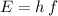where
`h` is Planck's Constant.

`h \approx 6.67 * 10^(-34)\; \rm m^2\cdot kg \cdot s^(-1)`.

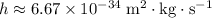This question did not provide the frequency
`f` of this wave directly; the value of
`f` needs to be calculated from the wavelength
`\lambda` of this wave. Assume that this wave is travelling at the speed of light in vacuum:

`c \approx 3.00* 10^(8)\; \rm m \cdot s^(-1)`.

The frequency of this electromagnetic wave would be:

`\begin{aligned}f &= (c)/(\lambda)\approx (3.00 * 10^(8)\; \rm m \cdot s^(-1))/(7.0 * 10^(-12)\; \rm m) \\ &\approx 4.29* 10^(19)\; \rm s^(-1) = 4.29 * 10^(19)\; \rm Hz\end{aligned}`.

Apply the Planck-Einstein Relation to find the energy of a photon of this electromagnetic wave:

`\begin{aligned}E &= h \, f \\ &\approx 6.63 * 10^(-34)\; \rm m^2\cdot kg \cdot s^(-1) * 4.29 * 10^(19)\; \rm s^(-1) \\ &\approx 2.8 * 10^(-14)\; \rm m^2\cdot kg \cdot s^(-1) = 2.8 * 10^(-14)\; \rm J \end{aligned}`.

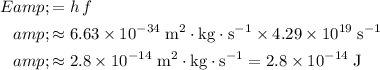Note that combining the two equations above (
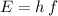`E = h \, f` and
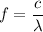`\displaystyle f = (c)/(\lambda)`) will give:

`\displaystyle E = h\cdot (c)/(\lambda)`.

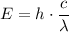This equation is supposed to give the same result (energy of a photon of this wave given its wavelength and speed) in one step:

`\begin{aligned}E &= h\cdot (c)/(\lambda) \\ &\approx 6.63 * 10^(-34) \; \rm m^2\cdot kg \cdot s^(-1)* (3.00* 10^(8)\; \rm m \cdot s^(-1))/(7.0 * 10^(-12)\; \rm m) \\ &\approx 2.8 * 10^(-14)\; \rm m\end{aligned}`.