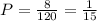Question

3 of the digits 0-9 are chosen randomly by a computer what is the probability that it will choose 3 sequential digits?

A.1/120
B.1/15
C.1/20
D.1/5040​

Answer 1

B. 1/15

Explanation:

The number of ways in which we can select x elements from a group of n elements is calculated as:

`nCx=(n!)/(x!(n-x)!)`

So, the number of ways in which a computer can select 3 digits is calculated as:

`10C3=(10!)/(3!(10-3)!)=120`

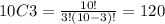
Because there are 10 digits from 0 to 9.

Then, from that 120 options there are 8 that have 3 sequential digits. These options are:

{0,1,2} {1,2,3} {2,3,4} {3,4,5} {4,5,6} {5,6,7} {6,7,8} {7,8,9}

So, the probability that it will choose 3 sequential digits is equal to:

`P=(8)/(120)=(1)/(15)`