Question

The volume of a sphere is 4,500π cubic yards. What is the radius of the sphere?

Answer 1

• 15

Explanation:

In the question it is given that the volume of a sphere is 4,500π cubic yards. And we have to find the radius.

We know that,

• 4/3πr³ = Volume of a sphere

Now, Substituting the values in the fomulae :

⇒ 4/3πr³ = 4500π

Cancelling π from both sides :

⇒ 4/3r³ = 4500

⇒ 4r³ = 4500 × 3

⇒ 4r³ = 13500

⇒ r³ = 13500/4

⇒ r³ = 3375

Taking cube root on both sides we get :

⇒ r = 15

Therefore,

• The radius of the sphere is 15 yards

Answer 2

• 15 yards

Explanation:

In this question we have provided volume of sphere that is 4500π cubic yards . And we are asked to find the radius of the sphere .

We know that ,

`\qquad \: \frak{Volume_((Sphere)) = (4)/(3)\pi r {}^(3) } \quad \bigstar`

Where ,

• r refers to radius of circle

Solution : -

As in the question it is given that volume of sphere is 4500π . So equation it with volume formula :

`\dashrightarrow \: \qquad \: (4)/(3) \pi r {}^(3) = 4500\pi`

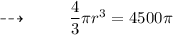
Step 1 : Cancelling π as they are present on both sides :

`\dashrightarrow \: \qquad \: (4)/(3) \cancel{\pi }r {}^(3) = 4500 \cancel{\pi}`

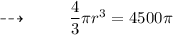
We get ,

`\dashrightarrow \: \qquad \: (4)/(3) r {}^(3) = 4500`

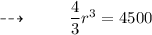
Step 2 : Multiplying with 3/4 on both sides :

`\dashrightarrow \: \qquad \: \frac{ \cancel{4}}{ \cancel{ 3}} r {}^( 3) * \frac{ \cancel{3}}{ \cancel{4}} = \cancel{ 4500} * \frac{3}{ \cancel{4} }`

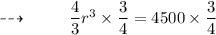
On further calculations, We get :

`\dashrightarrow \: \qquad \: r {}^(3) = 1125 * 3`

`\dashrightarrow \: \qquad \:r {}^(3) = 3375`

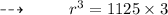
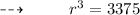
Step 3 : Applying cube root on both sides :

`\dashrightarrow \: \qquad \: \sqrt[3]{r {}^(3) } = \sqrt[3]{3375}`

We get :

`\dashrightarrow \: \qquad \: \purple{\underline{\boxed{\frak{r = 15 \: yards}}}}`

• Therefore , radius of sphere is 15 yards .

#Keep Learning