Question

A carpenter can do a job in eight hours. His assistant can do the same job in ten hours. How long would it take them to do the job together?

Answer 1

4.44

Explanation:

4.44

Answer 2

it will take them about 4.44 hours to complete the job when they work together

Explanation:

If carpenter B can complete the job in 8 hours, then the portion (fraction) of the job done in the unit of time (one hour) by this carpenter is 1/8

The assistant A can complete the same job in 10 hours, so the fraction of the job done by him in one hour is: 1/10

When they work together, we don't know what time it will take (we name it "x" hours). Therefore the fraction of the job dome in these x hours would be: 1/x

Now we can set the equation that says that the fraction of the job done by B in the unit of time plus the fraction done by A should equal the fraction completed when they work together:

`(1)/(8) +(1)/(10)=(1)/(x)\\(5)/(40) +(4)/(40)=(1)/(x)\\(9)/(40)=(1)/(x)\\\\x=(40)/(9) \\x=4.444...`

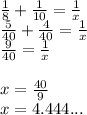
Therefore, it will take them about 4.44 hours to complete the job when they work together.