Question

886 randomly sampled teens were asked which of several personal items of information they thought it okay to share with someone they had just met. 44% said it was okay to share their e-mail addresses, but only 29% said they would give out their cell phone numbers. A researcher claims that a 2-proportion z-test could tell whether there was a real difference among all teens. Explain why that test would not be appropriate for these data.

Answer 1

Test statistic
`Z = 6.5217`

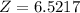
The Calculated value Z =6.5217 > 1.96 at 5% level of significance

Null hypothesis is rejected

There is real difference among all teens

Explanation:

Step(i):-

Given large sample size 'n' = 886

first sample proportion p⁻₁ = 44% =0.44

Second sample proportion p⁻₂ = 29% =0.29

Null hypothesis:H₀:There is no significant difference between two proportions

Alternative Hypothesis:H₁: There is significant difference between two proportions

Level of significance ∝ = 0.95 or 95%

`Z_{(\alpha )/(2) = Z_{(0.05)/(2) } = Z_(0.025) } =1.96`

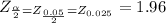
Step(ii):-

Test statistic

`Z = \frac{p^(-) _(1)-p^(-) _(2) }{\sqrt{pq((1)/(n_(1) ) +}(1)/(n_(2) ) )}`

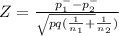
Where 'p'

`p = (n_(1) p^(-) _(1)+n_(2)p^(-) _(2) )/(n_(1) +n_(2) )`

`p = (886 (0.44)+886(0.29) )/(886+886 )`

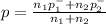
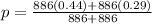
p = 0.365

q = 1-p =1-0.365 =0.635

`Z = \frac{0.44-0.29 }{\sqrt{0.365(0.635)((1)/(886) +}(1)/(886) )}`

`Z = (0.15)/( 0.023) = 6.5217`

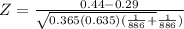
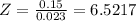
The Calculated value Z =6.5217 > 1.96 at 5% level of significance

Conclusion:-

Null hypothesis is rejected

There is real difference among all teens