Question

Which ordered pairs are in the solution set of the system of linear inequalities? y > Negative one-halfx y < One-halfx + 1

Answer 1

C

Explanation:

Answer 2

Option C.

Explanation:

The given system of linear inequalities is

`y>-(1)/(2)x`

`y<(1)/(2)x+1`

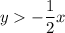
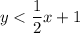
The related equations are

`y=-(1)/(2)x`

`y=(1)/(2)x+1`

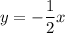
The above equations are 2 straight lines. The first dashed line has a negative slope and goes through (0, 0) and (4, negative 2). Everything above the line is shaded.

The second dashed line has a positive slope and goes through (negative 2, 0) and (2, 2). Everything below the line is shaded.

The shaded region represents the solution of given system of linear inequalities.

All the ordered pairs lies in the shaded region are the solution.

Consider the missing options are:

`(5, -2), (3, 1), (-4, 2)`

`(5, -2), (3, -1), (4, -3)`

`(5, -2), (3, 1), (4, 2)`

`(5, -2), (-3, 1), (4, 2)`

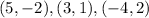
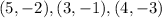
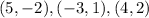
All ordered pairs
`(5, -2), (3, 1), (4, 2)` lie in the shaded region.

Therefore, the correct options is C.