Which function models the area of a rectangle with side lengths of 2x – 4 units and x + 1 units? What is the area when x = 3? A. f(x) = 2x^2 – 4x + 4; A = 10 B. f(x) = 2x^2 + 8x…

Question

asked Jan 7, 2021 218k views

1 Answer

Joe Simmons · Answer 1 · 2021-01-12T20:37:06+0000

Answer:

D. f(x) = 2x^2 − 2x − 4; A = 8

Explanation:

The area of a rectangle is given by the formula length x wide.

In this case we have that the length is 2x -4 and the wide is x +1

Therefore, the area will be:

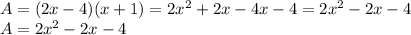
$A= (2x-4)(x+1)= 2x^2+2x-4x-4=2x^2-2x-4\\A= 2x^2-2x-4$

Now, when x = 3 we would have:

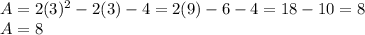
$A=2(3)^2-2(3)-4= 2(9)-6-4=18-10=8\\A=8$

Thus, the right answer is D.