Question

Which of the following is the complete list of roots for the polynomial function f(x) =

-(x2+2x–15)(x2+8x+17)
-5, 3
-5, 3, 4 + 1,4-i
-5, 3, 4 + i, 4 + 1
o 4+1, 4-1

Answer 1

Answer: -5, 3, 4 + 1,4-i (option 2)

Explanation:

The roots of an equation are the x values for f(x) = 0. Therefore to find the roots of the equation, you first set the function to 0 and then solve for the values of x.

since f(x) = -(x² + 2x - 15) (x² + 8x + 17)

0 = -(x² + 2x - 15) (x² + 8x + 17)

∴ either -x² - 2x + 15 = 0 OR x² + 8x +17 = 0

when -x² - 2x + 15 = 0

-x² - 5x + 3x + 15 = 0

(x - 3 ) (-x - 5) = 0

⇒ x = 3 or x = -5

when x² + 8x +17 = 0

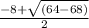`(-8 + √((64 - 68)))/(2)` = 0 OR
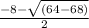`(-8 - √((64 - 68)))/(2)` = 0 (using the quadratic equation)

⇒ x = 4 + i or x = 4 - i

∴ the complete list of roots is -5, 3, 4 + 1,4-i (option 2)